PPC > EXEMPLES > Kakuro


TD Exercice 4


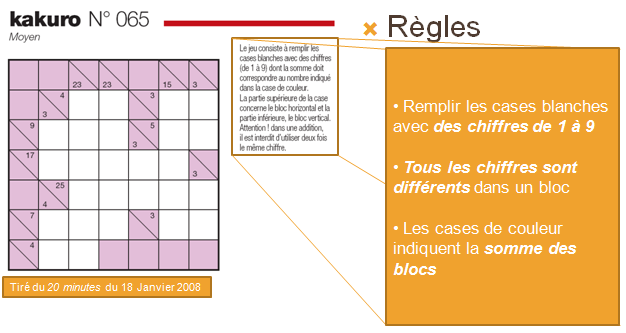
Modéliser le problème et trouver la solution au problème en utilisant le solveur Choco 2.0.

 

Solution Modèle 1

  • Pour chaque case blanche, une variable enumérée allant de 1 à 9.

  • Pour chaque bloc contigu :
    • Une contrainte linéaire (somme égale à la valeur fournie).
    • Des contraintes de différences.

Voici le code java en Choco 2.0 de ce premier modèle :

import choco.kernel.solver.variables.integer.IntDomainVar;
import choco.kernel.solver.ContradictionException;
import choco.kernel.model.Model;
import choco.kernel.model.variables.integer.IntegerVariable;
import choco.cp.model.CPModel;
import choco.cp.solver.CPSolver;
import choco.Choco;
import java.util.ArrayList;
import java.util.List;

public class Kakuro {

static int[][] instance = new int[][]{
new int[]{-1, -1, 2300, 2300, -1, 1500, 300},
new int[]{-1, 304, 0, 0, 3, 0, 0},
new int[]{9, 0, 0, 0, 305, 0, 0},
new int[]{17, 0, 0, 0, 0, 0, 300},
new int[]{-1, 425, 0, 0, 0, 0, 0},
new int[]{7, 0, 0, 0, 3, 0, 0},
new int[]{4, 0, 0, -1, -1, -1, -1}
};

public static void main(String[] args) {

// 0- Créons le modèle
Model m = new CPModel();

// 1- Créons les variables
IntegerVariable[][] vars;
vars = new IntegerVariable[instance.length][];
for (int i = 0; i < instance.length; i++)
{
int[] ll = instance[i];
vars[i] = new IntegerVariable[ll.length];
for (int j = 0; j < ll.length; j++)
{
int val = ll[j];
if (val == 0)
{
vars[i][j] = Choco.makeIntVar("x" + i + "_" + j, 1, 9);
}
}
}

int nbLig = instance.length;
int nbCol = instance[0].length;
for (int x = 0; x < nbLig; x++)
{
int y = 0;
while (y < nbCol)
{
while (y < nbCol && instance[x][y] < 0) y++;
if (y < nbCol)
{
if (instance[x][y] == 0) System.err.println("Probleme 1");
int sum = instance[x][y] % 100;
y++;
List<IntegerVariable> sumVars = new ArrayList<IntegerVariable>();
while (y < nbCol && instance[x][y] == 0)
{
sumVars.add(vars[x][y]);
y++;
}
if (sumVars.size() > 0)
{
IntegerVariable[] sumVars2 =
new IntegerVariable[sumVars.size()];
sumVars2 = sumVars.toArray(sumVars2);
m.addConstraint(Choco.eq(Choco.sum(sumVars2), sum));
postAlldiff(m, sumVars2);
}
}
}
}
for (int y = 0; y < nbCol; y++)
{
int x = 0;
while (x < nbLig)
{
while (x < nbLig && instance[x][y] < 0)
{
x++;
}
if (x < nbLig)
{
if (instance[x][y] == 0) System.err.println("Probleme 1");
int sum = instance[x][y] / 100;
x++;
List<IntegerVariable> sumVars = new ArrayList<IntegerVariable>();
while (x < nbLig && instance[x][y] == 0)
{
sumVars.add(vars[x][y]);
x++;
}
if (sumVars.size() > 0)
{
IntegerVariable[] sumVars2 = new IntegerVariable[sumVars.size()];
sumVars2 = sumVars.toArray(sumVars2);
m.addConstraint(Choco.eq(Choco.sum(sumVars2), sum));
postAlldiff(m, sumVars2);
}
}
}
}

CPSolver s = new CPSolver();
s.read(m);

try
{
s.propagate();
}
catch (ContradictionException e)
{ }

for(int x = 0; x < nbCol; x++)
{
for(int y = 0; y <nbLig; y++)
{
if (instance[x][y] == 0)
{
if (s.getVar(vars[x][y]).isInstantiated())
System.out.print(s.getVar(vars[x][y]).getVal());
else System.out.print("?");
}
else
{
System.out.print(" ");
}
}
System.out.println("");
}

s.solve();
System.out.println(s.pretty());
for(int x = 0; x < nbCol; x++)
{
for(int y = 0; y <nbLig; y++)
{
if (instance[x][y] == 0)
{
if (s.getVar(vars[x][y]).isInstantiated())
System.out.print(s.getVar(vars[x][y]).getVal());
else System.out.print("?");
}
else
{
System.out.print(" ");
}
}
System.out.println("");
}
s.printRuntimeSatistics();
}

private static void postAlldiff(Model m, IntegerVariable[] vars)
{
for(int i = 0; i < vars.length; i++)
{
for(int j = i+1; j < vars.length; j++)
{
m.addConstraint(Choco.neq(vars[i], vars[j]));
}
}
}

}


Solution Modèle 2

  • Objectif ==> une meilleure propagation : utilisation d'une contrainte dédiée.
  • Pour cela, on utilise une contrainte générique avec test :
    • Vérification qu’une valeur apparait une seule fois.
    • Vérifier la somme.

Voici le code java en Choco 2.0 de ce second modèle :

import choco.Choco;
import choco.cp.model.CPModel;
import choco.cp.solver.CPSolver;
import choco.kernel.model.Model;
import choco.kernel.model.variables.integer.IntegerVariable;
import choco.kernel.solver.Solver;
import choco.kernel.solver.constraints.integer.extension.LargeRelation;
import choco.kernel.solver.constraints.integer.extension.TuplesTest;

import java.util.ArrayList;
import java.util.BitSet;
import java.util.List;

public class KakuroAC {

static int[][] instance = new int[][]{
new int[]{-1, -1, 2300, 2300, -1, 1500, 300},
new int[]{-1, 304, 0, 0, 3, 0, 0},
new int[]{9, 0, 0, 0, 305, 0, 0},
new int[]{17, 0, 0, 0, 0, 0, 300},
new int[]{-1, 425, 0, 0, 0, 0, 0},
new int[]{7, 0, 0, 0, 3, 0, 0},
new int[]{4, 0, 0, -1, -1, -1, -1}
};

public static void main(String[] args)
{
Model m = new CPModel();
// 1- créons les variables
IntegerVariable[][] vars;
vars = new IntegerVariable[instance.length][];
for (int i = 0; i < instance.length; i++)
{
int[] ll = instance[i];
vars[i] = new IntegerVariable[ll.length];
for (int j = 0; j < ll.length; j++)
{
int val = ll[j];
if (val == 0)
{
vars[i][j] = Choco.makeIntVar("x" + i + "_" + j, 1, 9);
}
}
}

int nbLig = instance.length;
int nbCol = instance[0].length;

for (int x = 0; x < nbLig; x++)
{
int y = 0;
while (y < nbCol)
{
while (y < nbCol && instance[x][y] < 0) y++;
if (y < nbCol)
{
if (instance[x][y] == 0) System.err.println("Probleme 1");
int sum = instance[x][y] % 100;
y++;
List<IntegerVariable> sumVars =
new ArrayList<IntegerVariable>();
while (y < nbCol && instance[x][y] == 0)
{
sumVars.add(vars[x][y]);
y++;
}
if (sumVars.size() > 0)
{
IntegerVariable[] sumVars2 =
new IntegerVariable[sumVars.size()];
sumVars2 = sumVars.toArray(sumVars2);
postConstraint(m, sumVars, sum);
}
}
}
}
for (int y = 0; y < nbCol; y++)
{
int x = 0;
while (x < nbLig)
{
while (x < nbLig && instance[x][y] < 0) x++;
if (x < nbLig)
{
if (instance[x][y] == 0) System.err.println("Probleme 1");
int sum = instance[x][y] / 100;
x++;
List<IntegerVariable> sumVars =
new ArrayList<IntegerVariable>();
while (x < nbLig && instance[x][y] == 0)
{
sumVars.add(vars[x][y]);
x++;
}
if (sumVars.size() > 0)
{
IntegerVariable[] sumVars2 =
new IntegerVariable[sumVars.size()];
sumVars2 = sumVars.toArray(sumVars2);
postConstraint(m, sumVars, sum);
}
}
}
}

Solver s = new CPSolver();
s.read(m);
s.solve();
System.out.println(s.pretty());
for(int x = 0; x < nbCol; x++)
{
for(int y = 0; y <nbLig; y++)
{
if (instance[x][y] == 0)
{
if (s.getVar(vars[x][y]).isInstantiated())
System.out.print(s.getVar(vars[x][y]).getVal());
else System.out.print("?");
}
else
{
System.out.print(" ");
}
}
System.out.println("");
}
s.printRuntimeSatistics();
}

private static void postConstraint(Model m,
List<IntegerVariable> sumVars, final int sum)
{
IntegerVariable[] vars = new IntegerVariable[0];
vars = sumVars.toArray(vars);
m.addConstraint(
Choco.relationTupleAC(vars, new TuplesTest()
{
public boolean checkTuple(int[] tuple)
{
int s = 0;
BitSet bs = new BitSet();
for (int v : tuple)
{
if (bs.get(v)) return false;
bs.set(v);
s += v;
}
return s == sum;
}
})
);
}
}

Voici le plan de cette présentation sur la programmation par contraintes

Cette page a été co-réalisée avec Guillaume Rochart, docteur en mathématiques dans mon équipe de recherche au Bouygues e-lab.10/03/2009.