PPC > EXEMPLES > N Reines



TD Exercice 1

Placer sur un échiquier de taille n, n reines telles qu’aucune d’entre elles ne soit en prise.

Modéliser le problème et trouver la solution au problème en utilisant le solveur Choco 2.0.

 

Solution Modèle 1

Comment modéliser le problème avec les contraintes déjà évoquées ?

On associe à chaque ligne une variable précisant la position de la reine dans le ligne

  • Une variable énumérée par ligne : X1=[[1,n]] …
  • Une reine par ligne (c’est évident)
  • Une reine par colonne :
    • allDifferent(X1, X2, … Xn)
  • Une reine par diagonale :
    • allDifferent(X1+1, X2+2, … Xn+n)
    • allDifferent(X1-1, X2-2, … Xn-n)

Modèle plus classique en PPC : moins de variables et moins de contraintes

Voici le code java en Choco 2.0 de ce premier modèle :

import choco.kernel.model.Model;
import choco.kernel.model.variables.integer.IntegerVariable;
import choco.kernel.solver.Solver;
import choco.cp.model.CPModel;
import choco.cp.solver.CPSolver;
import choco.Choco;

public class NReinesModel1 {

public static final int NB_REINES = 10;

public static void main(String[] args) {

// 0. Création du problème
Model m = new CPModel();

// 1. Création des variables
IntegerVariable[] vars = createVariables(m);

// 2. Création des contraintes
postConstraints ( m, vars );

// 3. Choix solver et heuristique
Solver s = new CPSolver ();
s.read(m);
setHeuristic(s);

// 4. Résolution du problème
s.solve();

// 5. Récupérer la solution
displayResult(s, vars);
}

// 1. Création des variables
private static IntegerVariable[] createVariables(Model m) {
IntegerVariable[] vars = new IntegerVariable[NB_REINES];
for (int i = 0; i < NB_REINES; i++) {
vars[i] = Choco.makeIntVar("x" + i, 0, NB_REINES - 1);
}
return vars;
}

// 2. Création des contraintes
private static void postConstraints(Model m, IntegerVariable[] vars) {
postConstraints1(m, vars);
postConstraints2(m, vars);
}

// 2.1. Une reine par colonne
private static void postConstraints1(Model m, IntegerVariable[] vars) {
for(int i = 0; i < NB_REINES; i++) {
for(int j = i+1; j < NB_REINES; j++) {
m.addConstraint( Choco.neq(vars[i], vars[j]) );
}
}
}

// 2.2. Une reine par diagonale
private static void postConstraints2(Model m, IntegerVariable[] vars) {
for (int i = 0; i < NB_REINES; i++) {
for (int j = i + 1; j < NB_REINES; j++) {
int k = j - i;
m.addConstraint(Choco.neq(vars[i], Choco.plus(vars[j], k)));
m.addConstraint(Choco.neq(vars[i], Choco.minus(vars[j], k)));
}
}
}

// 3. Réglage de l'heuristique de choix de valeurs
private static void setHeuristic(Solver s) {
s.setValIntIterator(new DecreasingDomain());
}

// 5. Affichage des résultats
private static void displayResult(Solver s, IntegerVariable[] vars) {
if (s.getNbSolutions() > 0) {
System.out.println("Solution trouvŽe : ");
for (int i = 0; i < NB_REINES; i++) {
int val = s.getVar(vars[i]).getVal();
for (int j = 0; j < NB_REINES; j++) {
System.out.print(val == j ? "R " : ". ");
}
System.out.println("");
}
} else {
System.out.println("Pas de solution trouvŽe !!");
}
}

 

Solution Modèle 2

On associe à chaque case un booléen (reine présente ou non)

Xij = { 0,1 } avec 0 pas reine, 1 une reine

Une reine par ligne :

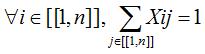
De même pour les colonnes et les diagonales (partielles ou non).

Modèle classique à la Programmation Linéaire.

Voici le code java en Choco 2.0 de ce second modèle :

import choco.kernel.model.Model;
import choco.kernel.model.variables.integer.IntegerVariable;
import choco.kernel.solver.Solver;
import choco.cp.model.CPModel;
import choco.cp.solver.CPSolver;
import choco.cp.solver.search.integer.valiterator.DecreasingDomain;
import choco.Choco;

import java.util.List;
import java.util.ArrayList;

public class NReineModele2 {

public static final int NB_REINES = 10;

public static void main(String[] args) {

long time = System.currentTimeMillis();

System.out.println("NReine mod?le 1");

// 0. Création du problème
Model m = new CPModel();

// 1. Création des variables
IntegerVariable[] vars =
createVariables(m);

// 2. Création des contraintes
postConstraints(m, vars);

// 3. Choix solver et heuristique
Solver s = new CPSolver();
s.read(m);
setHeuristic(s);

// 4. Résolution du problème
s.solve();

// 5. Récupération de la solution
displayResult(s, vars);

System.out.println("Time ellapsed: " + (System.currentTimeMillis() - time) + "ms.");
}

// 1. Création des variables
private static IntegerVariable[] createVariables(Model m) {
IntegerVariable[] vars = new IntegerVariable[NB_REINES * NB_REINES];
for (int i = 0; i < NB_REINES; i++) {
for (int j = 0; j < NB_REINES; j++) {
vars[index(i, j)] = Choco.makeIntVar("x" + i + "_" + j, 0, 1);
}
}
return vars;
}

// 2. Création des contraintes
private static void postConstraints(Model m, IntegerVariable[] vars) {
postConstraints1(m, vars);
postConstraints2(m, vars);
}

// 2.1. Une occurence par ligne et par colonne
private static void postConstraints1(Model m, IntegerVariable[] vars) {
IntegerVariable one = Choco.makeConstantVar("one", 1);
for (int i = 0; i < NB_REINES; i++) {
IntegerVariable[] col = new IntegerVariable[NB_REINES];
IntegerVariable[] line = new IntegerVariable[NB_REINES];
for (int j = 0; j < NB_REINES; j++) {
col[j] = vars[index(i, j)];
line[j] = vars[index(j, i)];
}
m.addConstraint(Choco.occurrence(1, one, col));
m.addConstraint(Choco.occurrence(1, one, line));
}
}

// 2.2 Une occurence par diagonale
private static void postConstraints2(Model m, IntegerVariable[] vars) {
IntegerVariable one = Choco.makeConstantVar("one", 1);
for (int diag = 0; diag < 2 * NB_REINES - 1; diag++) {
List<IntegerVariable> diag1 = new ArrayList<IntegerVariable>();
List<IntegerVariable> diag2 = new ArrayList<IntegerVariable>();
for (int i = 0; i < NB_REINES; i++) {
int index1 = index(i, i + diag - NB_REINES + 1);
int index2 = index(NB_REINES - i - 1, i + diag - NB_REINES + 1);
if (index1 >= 0 && index1 < NB_REINES * NB_REINES) {
diag1.add(vars[index1]);
}
if (index2 >= 0 && index2 < NB_REINES * NB_REINES) {
diag2.add(vars[index2]);
}
}
m.addConstraint(Choco.occurrenceMax(1, one, diag1.toArray(new IntegerVariable[]{})));
m.addConstraint(Choco.occurrenceMax(1, one, diag2.toArray(new IntegerVariable[]{})));
}
}

// 3. Réglage de l'heuristique
private static void setHeuristic(Solver s) {
s.setValIntIterator(new DecreasingDomain());
}

// 5. Affichage des résultats
private static int index(int i, int j) {
if (i < 0 || i >= NB_REINES) return -1;
if (j < 0 || j >= NB_REINES) return -1;
return i * NB_REINES + j;
}

// 5. Affichage des résultats
private static void displayResult(Solver s, IntegerVariable[] vars) {
if (s.getNbSolutions() > 0) {
System.out.println("Solution trouvée : ");
for (int i = 0; i < NB_REINES; i++) {
for (int j = 0; j < NB_REINES; j++) {
System.out.print(s.getVar(vars[index(i, j)]).getVal() == 1 ? "R " : ". ");
}
System.out.println("");
}
}
else {
System.out.println("Pas de solution trouvée !!");
}
}


}

 

Voici le plan de cette présentation sur la programmation par contraintes

Cette page a été co-réalisée avec Guillaume Rochart, docteur en mathématiques dans mon équipe de recherche au Bouygues e-lab.10/03/2009.